前言

我们都遇到过如下计算结果：

1	0.1 + 0.2 = 0.30000000000000004;

为什么会出现如此结果？难道不为 0.3 吗？这涉及到 js 的精度问题。

首先 js 的数字类型采用基于 IEEE 754 标准来实现的（也称为浮点数）。其选用的精度格式是：双精度格式（64 位的二进制数）

这篇就稍稍深入了解下双精度浮点数，以及有关于数 Number 的问题。

IEEE 754 标准

IEEE 二进制浮点数算术标准（IEEE 754），是最广泛使用的浮点数运算标准，为许多 CPU 与浮点运算器所采用。

这个标准定义了表示浮点数的格式（包括负零-0）与反常值（denormal number），一些特殊数值（（无穷（Inf）与非数值（NaN）），以及这些数值的“浮点数运算符”；它也指明了四种数值舍入规则和五种例外状况（包括例外发生的时机与处理方式）。

规定了四种表示浮点数值的方式：单精确度（32 位）、双精确度（64 位）、延伸单精确度（43 比特以上，很少使用）与延伸双精确度（79 比特以上，通常以 80 位实现）

当然我们只讨论 js 中的 64 位的双精度 方式。

64 位的双精度

下图基本解释清楚 64 位数的组成部分：

sign bit（S 符号）：符号位，表示正负号（0 为负数，1 为正数）
exponent（E 指数）：表示次方数，在（二进制的）科学计数法中定义 2 的多少次幂
mantissa（M 尾数）：表示精确度（小数部分，规范中会省略个位数上的 1 ）

那么一个双精度值的表达式如下：

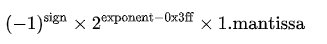
我们下面来具体解释一下。

符号位 sign

符号位很容易理解，表示整个数的正负值。

1 2	Math.pow(-1, 0); //1 Math.pow(-1, 1); //-1

所以用此位来示意数的正负性。

尾数位 mantissa

尾数也被称为规约形式的浮点数，因为在科学计数法的显示下，分数（fraction 也是 mantissa 那个部分之一）部分最高有效为是 1 （个位数）

1 2	1000.001(2) 2^3 * 1.000001(科学计数法表示)

最终 mantissa 会以 000001 来示意，会被规范成 1.M 格式 ，其中 1 会被隐藏掉，所以最大是表达 53 位的数（如上图，实际 mantissa 只有 52 位）。

指数位 exponent

科学计数法

我知道各位都是受过义务教育的，不过我真的忘记了，简单回顾下把：

科学记数法是一种记数的方法。把一个数表示成 a 与 10 的 n 次幂相乘的形式（1≤|a|<10，n 为整数），这种记数法叫做科学记数法。

1
2
3

// 科学记数法
100; // 1*10^2
0.001; // 1*10^-3

那和科学计数法有什么关系，应该注意到 指数位是 2 的 n 次幂 （为何不是 10 ，因为是二进制）。

如果我们要表达 100(2)，则结果如下：

1	100(2); // 1*2^2

指数偏移值（exponent bias）

我们了解科学计数法是可以表示大于 1 ，或者小于 1 的数（小数），即：通过正负指数的值来标识显示。

由于指数位的 11 位不包括符号位，那么为了达到这样正负的效果，就引入了 指数的偏移值。

为什么要引入这个概念？我想了很久，以下这个例子或许会给你启发：

指数如果是 1023 和 1024，到底哪个值谁大？

首先 11 位的指数位对应的二进制最大和最小结果值为：00000000000(0) ，11111111111(2047，2^(12-1)-1)，即指数的取值范围为：[0,2047]

并且我们知道指数具有 正负值 （来控制小数点左右移位），那么我们按照二进制中负数的规则（取反，补位），那么指数值为 [0,1023] 区间内为正数，[1024,2047] 内为负数（二进制中负数最高位为 1 ）。

# 补充下：为何负数是从 1024 开始？
011 11111111 # 1023

# 如果该二进制再继续增大，就进入了负数区域（最高位为 1）
100 00000000 # 1024

另外，根据 IEEE 规范， 0 和 2047 两个最值需要做特殊用途，所以这里移除，所以整个规范的指数取值范围是： [1,2046]

回到这个问题，1023 和 1024 到底谁大，按照上面区间的划分，明显是 1023 > 1024 （正数大于负数，但机器不那么想）。

崩溃！就我个人理解起来就很困难，更不谈实际运算了（当你看到一个大于 1023 的值，还需要引入符号位，补码之类的计算方式）。

所以引入偏移值 bias（bias = 1023），使得整个运算简单，好理解。

那么 [-1022+bias,1023+bias] 等同于 [1,2046]，这样抛去了符号位的影响，最终：1023 就变成了 0 ，1024 变成了 1 ，明显 1 的指数值更大。

至于为何是 1023 ，我给的建议是 2046/2 （虽然这样理解是不对的），另外 32 位精度浮点数的偏移量是 127 。

参考

举例

4.5 (10) 
100.1 (2)
1.001 * 2^2
符号位：0 (正数)
指数：1025 (2+1023)
尾数：001 (注意，1 省略)

标准（规格）和非标准（规格）

整个指数位的值分为三种情况：

名称	指数 E	加偏移值（exponent bias）	尾数 M	表示
规格化	[1,2046]	[-1022,1023]	1.M（含有隐藏位 1）
非规格化	0	-1023	0	±0 非常接近 0 的数
非规格化	2047	1023	0	±∞
非规格化	2047	1023	非 0	NaN

解惑些问题

整数范围

当尾数为标准模式时：1.M ，尾数位供 52 位，加上隐藏位 1 ，整个精度会是 53 位。

那么整数的取值范围是 [-2^53-1,2^53-1]

1 2	(Math.pow(2, 53) - 1 == Number.MAX_SAFE_INTEGER; //9007199254740992 - (Math.pow(2, 53) - 1)) == Number.MIN_SAFE_INTEGER;//-9007199254740992

最小精度

在尾数的 52 位中，使得有一个最小的位定义（1.00000~ 中间 51 个 0~00001），即 2^-52 。

1	Math.pow(2, -52) == Number.EPSILON; //2.220446049250313e-16

0.1+0.2 等于什么？

按照最小精度，即打满 52 位，那么像 0.1 和 0.2 最终无限循环后的：

1
2
3

0.0001100110011001100110011001100110011001100110011001101 + 0.0011001100110011001100110011001100110011001100110011010 = 0.0100110011001100110011001100110011001100110011001100111;

等于：0.30000000000000004.toString(2)

最后

对于这个 IEEE 754 规范，我理解的还不是很透彻，不过对于 js 精度上的问题也算是有个初步的解答。

如果有不对之处望各位留言指正。